PROBABILITAS 2

hai semuanya... kali ini kita bakal bahas lagi nih tentang PROBABILITAS 2 yuk kita belajar
bersama-sama lagiii:)

PROBABILITAS 2

1.Probabilias Marjinal
   Di dalam praktik kita sering kali menjumpai suatu kejadian yang terjadi bersamaan dengan kejadian lainnya,dimana kejadian lainnya tersebut dipengaruhi kejadian yang pertama.
Apabila pemilik pabrik tersebut mengambil 1 batrai secara acak ,berapa probabilitasnya bahawa batrai yang diambil tersebut rusak.
   P(R) = probabilitas barang rusak, disebut probabilitas marjinal
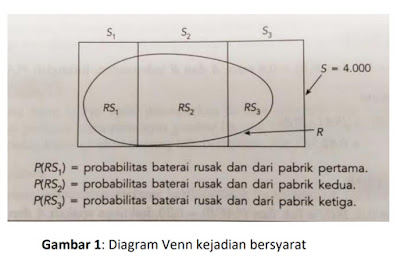
Baterai yang rusak tersebut dapat berasal dari pabrik pertama ,kedua dan ketiga untuk menjawab pertanyaan itu,perhatikan gambar dibawah ini

Karena P(RS1) = P(S1)P(R/S1) kita peroleh rumus berikut:
Probabilitas Marjinal = P(R) = ∑ 𝑃(S1)P(R/S1) (1)
Dengan rumus tersebut, kita dapat menghitung probabilitas bahwa baterai yang dipilih
secara acak rusak, yaitu:

2. Teorema Bayes
     Thomas Bayes (1702-1761) mengembangkan teori untuk menghitung probabilitas tentang sebab-akibat (cause) dari suatu kejadian berdasarkan pengaruh yang dapat diperoleh sebagai observasi.“Bayesian decision theory” yaitu teori keputusan
berdasarkan perumusan Thomas Bayes yang bertujuan untuk memecahkan masalah
pembuatan keputusan yang mengandung ketidakpastian (decision making under
uncertainly).

3. Permutasi dan Kombinasi
Seperti telah kita ketahui, suatu eksperimen akan memberikan hasil eksperimen
(outcome). Setiap hasil eksperimen dapat dianggap sebagai suatu titik, sehingga
kumpulan hasil ekperiman tersebut dinamakan titik-titik sampel (sample point). Setiap
titik tadi disebut elemen, sedangkan seluruh elemen disebut ruang sampel (sample
space). Kejadian sebetulnya terdiri dari kumpulan elemen tersebut.
Suatu eksperimen yang dilakukan dalam beberapa langkah (steps), dimana setiap
langkah menghasilkan berbagai kemungkinan hasil (outcome) yang berbeda, diperlukan
suatu cara atau aturan untuk menghitung seluruh hasil. Apabila langkah pertama dari
suatu eksperimen dapat menghasilkan k hasil (outcome) yang berbeda sedangkan
langkah kedua menghasilkan m hasil yang berbeda, maka keseluruhan eksperimen yang
terdiri dari 2 langkah tersebut akan menghasilkan k • m hasil.

Misalkan seorang direktur pemasaran mempunyai 4 alternatif didalam memasang iklan
(Koran, majalah, TVRI, RRI) dan 2 kemungkinan rancangan pembungkus (packaging
design), yaitu memakai botol plastic dan kotak karton. Banyaknya kombinasi iklan dan
rencana pembungkusan = k • m = 4 x 2 = 8. Kalau dinyatakan dalam diagram pohon,
gambarnya dapat dilihar pada peraga 10. Apabila pada salah satu langkah dalam
eksperimen menghasilkan m hasil yang berbeda dan langkah ini terjadi sampai k kali,
PERMUTASI adalah suatu pengaturan atau urutan beberapa elemen atau objek
(misalnya hasil suatu eksperimen), dimana urutan itu penting, maksudnya 123 tidak
sama dengan 213, ABC ≠ BCA, dan seterusnya.

Perbedaan Permutasi dan Kombinasi
Salah satu perbedaan antara Permutasi dan Kombinasi adalah jika Permutasi maka
perbedaan urutan menjadikan perbedaan makna, sementara di Kombinasi perbedaan
urutan tidak akan menjadikan perbedaan makna. Contoh: {a,b,c} pengambilan 2 unsur
dari 3 unsur jika menggunakan permutasi maka akan diperoleh hasil ab, ba, ac, ca, bc,
cb. Tetapi jika menggunakan kombinasi hasil yang diperoleh adalah ab, ca, bc.